8. 速度波形および変位波形の求め方
8.1 これまでに提案された方法
(1) 直接積分
適当な初期条件のもとで,加速度波形を直接に積分する方法である。
結果は,多くの場合異常に大きな最大値が得られ,波形も誤差によると思われる長周期成分が卓越することが多い。
(2) 栗原・桜井の検討
栗原・桜井は,それまでに提案されていた多項式による補正法と低振動数成分を取除くフィルタによる補正法とを,振動台による加振例に適用している。その結果をもとに補正法の評価を行なった18)。
多項式による補正法とは,高々10次程度の多項式をゼロ線として仮定し,補正後の速度の2乗平均値または変位の2乗平均値を最小とするように多項式の係数を定めて補正する方法である。
また,栗原・桜井の検討したフィルタG1(f)は,振動数をf,実数のパラメタをλとして,次式で表わされる。
.png) ・・・ (8-1)
・・・ (8-1)
ただし,iは虚数単位,πは円周率である。このフィルタを,速度を求める段階で1度,さらに,変位を求める段階でもう一度かけながら,積分を行なう。
2回積分と合成した形で,このフィルタを図-8.1に示す。
これらの方法について,栗原・桜井が検討した結果,多項式による補正よりもフィルタによる補正の方がよい結果を与えるが,このフィルタでもパラメタをどのように選んでも,ドリフト除去と真の波形の抽出とが競合することが指摘された。
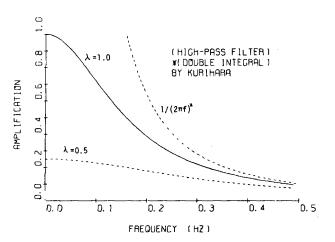
図-8.1 栗原・桜井のフィルタと2回積分の合成
(3) Trifunacの方法
Trifunacの提案した方法は,基本的には,フィルタにより低振動数成分を取除く方法であり,フィルタG2(f)は,f1,f2をパラメタ,fを振動数として,次式で表わされる19)。
.png) ・・・ (8-2)
・・・ (8-2)
ここで,彼は,低振動数の誤差の検討をもとに,f1=0.05(Hz),f2=0.07(Hz)とすることを提案した。図-8.2に2回積分と合成した形でこのフィルタを示す。なお,フィルタをかける前にフィルタによって除くことのできない誤差を除くため,加速度及び速度に,最小自乗法による直線のあてはめを行なっている。
さらに,この方法を数多くの記録に適用するに当って,若干の改良が加えられた20),21)。改良された点は,フィルタをかけるに当って,数字化された区間の外側に適当なデータを補うことにより,区間端で発生する恐れのあるフィルタの応答をおさえるものである。
1973年になって,数字化のために分割された区間の短い記録の場合には,f2=0.125(Hz)を適用することに変更された22)。
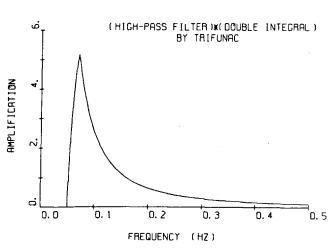
図-8.2 Trifunacのフィルタと2回積分の合成
USGSでは,この方法をもとにさらにf2の決定について,数字化された記録の全長が60秒以下の場合には,f2として,その全長の1/4の逆数をとるという条件を加えた23)。また,f1もf2に合わせて適宜変更されている。
今西・後藤・亀田は,このフィルタをSMAC-B2強震計の記録に適用するためいくつかの事例研究を行ない,f2の値として,0.1(Hz)程度とすることを提案した24)。
この方法についての評価は,Trifunac,Lee,Hanksによって行なわれた22),25)。この評価は,得られた変位波がどの程度真の変位波形に近いかという観点からではなく,得られた変位波形と真の変位波形を仮に同じフィルタを通して得られる仮想の波形とがどの程度相互に似ているかという観点からなされた。したがって,この観点からすれば,フィルタによって取去る振動数範囲を大きくするほど,"誤差"が小さいことになり,地震計の感度が約8cm/gの記録では,
f2=0.07〜0.1 (Hz)のとき 2〜4cm程度
f2=0.1(Hz)のとき 2cm程度
f2=0.125〜0.2(Hz)のとき 1cm程度
の誤差があるという評価を彼らは行なった。
一方,得られた変位波がどの程度真の変位波に近いかという点についても,TrifunacとLeeによって評価が行なわれたが,わずか1つの地震記録の例について行なわれたのみである25)。この結果は震源から約80kmの地点で,周期4.1秒,減衰定数0.59の地震計で得られた記録から求めた変位波形では,f2を1/8(Hz)から1/50(Hz)の範囲で変えても,結果に及ぼすf2の影響は小さかった。このことから,震源距離が十分に大きく,マグニチュードがこの地震の程度の大きさであれば,この方法により求めた変位波形は,真の変位波形に十分近いという評価を彼らは与えている。
(4) 田中,森下,大沢,吉沢の方法
この方法も,フィルタにより低振動数成分を取除く方法である。フィルタG3(f)は次式で表わされる26),27)。
.png) ・・・ (8-3)
・・・ (8-3)
ここに、f3=0.005(Hz)
f4=0.1(Hz)
このフィルタと2回積分を合成したものを図-8.3に示す。
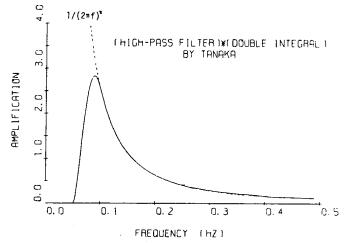
図-8.3 田中のフィルタと2回積分の合成
(5) 倉田・土田の方法
この方法も,フィルタによる方法である28)。この方法は,気象庁の1倍地震計(固有周期6秒,減衰定数55%)のシュミレーションに加えて,先に述べた栗原・桜井により検討されたフィルタG1(f)を補助的に使うものである。補助的に使うフィルタG1(f)は速度を求める段階で1度,さらに,変位波を求める段階でもう一度加えながら積分を行なう。すなわち,変位を求める段階までにかけられるフィルタG4(f)は,次式で表わされる。
.png) ・・・ (8-4)
・・・ (8-4)
ここに、f5=1/6(Hz)
h=0.55
λ0=0.2π
このフィルタを,2回積分との合成で図-8.4に示す。
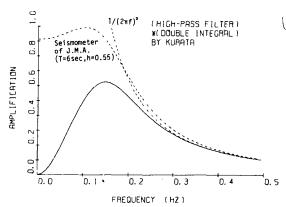
図-8.4 倉田のフィルタと2回積分の合成
(6) 久保・佐藤の方法
この方法は,補正のため取除く加速度成分の最大値を一定に保ちながら,補正された速度振幅の2乗和を最小とするものである29)。なお,あらかじめ直線により,速度振幅の2乗和を最小とするように補正を行なっておく。補正のため取除く加速度成分の最大値は,対象とする加速度波形の最大加速度の約1%とされている。
この方法についての評価は,提案者自身により行なわれ,1つの記録の例について固有周期2秒の変位計の地震記録と比較され,固有周期2秒の変位計の記録は,この方法により十分推定できるという評価を与えている。29)
なお,あらかじめ直線により,速度振幅の2乗和を最小とするように補正を行なっておく。補正のため取除く加速度成分の最大値は,対象とする加速度波形の最大加速度の約1%とされている。
この方法についての評価は,提案者自身により行なわれ,1つの記録の例について固有周期2秒の変位計の地震記録と比較され,固有周期2秒の変位計の記録は,この方法により十分推定できるという評価を与えている29)。
8.2 各種方法の比較と評価
(1) 多項式による補正法の振動数領域における解釈
これまでに提案された方法は,フィルタによって振動数成分を取除くという方法が多い。そこで,フィルタによらない方法についても,振動数領域における解釈を行なった方が,相互比較の上で便利であると思われる。そこで,まず多項式による補正法の振動数領域における解釈をしておく。
補正に用いる多項式は時間をtとして
.png) ・・・ (8-5)
・・・ (8-5)
なる関数に,係数をかけて加えたものである。xn(t)のフーリエ変換をXn(f)(fは振動数)とすれば,
.png) ・・・ (8-6)
・・・ (8-6)
(ここに、i は虚数単位)
部分積分により,
.png) ・・・ (8-7)
・・・ (8-7)
したがって,多項式による補正というのは,振動数領域においては,おおむね,1/fl(lは1以上の整数)に適当な係数をかけたものの和の形で低振動数成分を取去るものであると言えよう。
(2) 久保・佐藤の方法の振動数領域における解釈
久保・佐藤の方法は,取去る振動数成分の大きさを最大加速度の形で規定し,補正後の速度の2乗平均値を最小とするように補正を行なうというものである。
取去る振動数成分の大きさを最大加速度の形で測るという条件は,振動数領域においては,取扱いが難しいので,ここではひとまず,取去る振動数成分の大きさを,加速度波形の形での2乗平均値で測るものとして,検討を進める。加速度波形の2乗和は,加速度波形のフーリエ変換の絶対値の2乗を振動数について積分したものに等しいので,この形であれば取扱いが易しくなるからである。
今,加速度振幅の等しい2つの正弦波振動を考え,それぞれの振動数をf1,f2(ただし,f1,<f2)とする。この2つの正弦波振動の速度振幅は,当然,振動数の低い振動数f1の振動の方が大きい。したがって,加速度振幅の等しい2つの正弦波を別のある加速度波形に加える場合,その速度振幅に与える影響は,振動数の低い正弦波の方が大きい。言いかえれば,加速度の大きさに対して速度振幅に与える影響の大きさを考えた場合,低振動数であるほど効率が高い。
このことから,加速度波形の2乗平均値が一定であるよう様々な波形のうち,別のある加速度波形との差によって求められた波形の加速度振幅の2乗平均値を最小とするような波形は,「別のある加速度波形」の低振動数部分に等しいと考えられる。その振動数の範囲は,その低振動数部分の加速度波形としての2乗平均値が,先に述べた規定値に等しいという条件で定まる。言いかえれば,取去る加速度成分の2乗平均値が一定であるという条件の下で,補正された速度波形の2乗平均値を最小にするという方法は,振動数領域においては,ある振動数を境界として,その振動数以下の振動数成分を取去るようなフィルタを用いるという方法と同じである。この境界の振動数は,地震波ごとに取去る低振動数成分の量を規定することにより,定まるわけである。
取去る低振動数成分の大きさを最大加速度の形で規定した場合には,2乗平均値で規定した場合とはやや異なり,境界付近の取去り方がやや異なってくるのと同時に,高い振動数の成分にもやや影響を及ぼすものと思われるが,全体として見れば,その相異の程度は小さいものと思われる。したがって,久保・佐藤の方法は,地震波によって定まるパラメタを持つフィルタによる補正方法と等価であるものと思われる。
(3) 多項式による方法とフィルタによる方法の比較
多項式による補正方法は,先に述べたように,振動数をfとすれば,1/fl (l=1,2,3・・・・・)の形の1次結合の形に,取去る成分を規定して行なう。何故このような形に規定するかの根拠は,それほど明らかではない。積分において異常に卓越する振動数成分は,低い振動数成分であるから,多項式のよる補正における誤差の形に関する条件がないという点で,フィルタによる方法の方が自由度があり,かつ自然であると言えよう。
(4) フィルタの形
フィルタについて検討すべき点としては,1つはどの程度の振動数範囲を取去るかという点であり,もう1つは取去る部分との境界付近の振動数において,どの程度はっきりとした境界を作ったらよいかという点である。ここでは,後者についての検討を行なう。
検討においては,加速度波形と,フィルタを通しかつ積分して求められた変位波形との関係を直接に見ることができるという配慮から,フィルタと2回積分との合成の形で検討を行なった。ここで検討を行なうのは,フィルタの形であるから,フィルタとしては例えばその等価帯域幅のような形で,取去る振動数範囲は一致させておくべきであろうが,既に示した図-8.1〜図-8.4によっても,この点を注意しておけば,比較は可能であると判断し,改めて正規化した図は示さないこととした。
図-8.2に示したTrifunacのフィルタは,著しいピークを持つので,このピーク振動数付近の振動数成分が,このフィルタによって人工的に卓越させられる恐れが大きい。他のフィルタと比べて特にこの傾向が著しいので,フィルタの形としては最適であるとはいえない。しかし,振動数軸上の境界が明瞭であるから,振動数軸上での検討には便利である。
図-8.1に示した栗原・桜井によって検討されたフィルタはTrifunacのフィルタとは逆に,波形の性質をゆがめる度合が小さいという点では,4つのフィルタのうち最も望ましい。しかし,栗原・桜井による検討では,0Hz付近の成分の取除き方がゆるやかすぎるので,ドリフトを除去しようとすれば,真の波形の成分も広い振動数範囲にわたって除去することになり,逆に真の波形の成分を残そうとすると,ドリフトの除去が十分にできなくなるという結果が得られた18)。著者らも,先に述べた倉田のフィルタを検討するにあたって,補助のフィルタを使わないで,一倍地震計のシュミレーションのみによる計算を行なったが,一倍地震計によるフィルタの形と似た性質を持つ栗原・桜井のフィルタについての検討結果と同様の結果を得た経験がある。したがって,このフィルタでは,ドリフト除去と真の波形の成分の抽出とが競合すると言える。
以上のことから,フィルタの形としてはTrifunacのフィルタと,栗原・桜井の検討したフィルタとの中間的な性質を持つ倉田のフィルタ(図-8.4)あるいは田中のフィルタ(図-8.3)が望ましい妥協点であると思われる。
(5) 取去るべき振動数の範囲
フィルタの形の検討に用いた4つのフィルタによる方法では,フィルタによって取去る振動数の範囲がそれぞれ固定されているが,久保・佐藤による方法では,その範囲が地震波ごとに異なって定められる。取去るべき振動数の範囲は,誤差の大きさと真の波形の大きさとの関係とともに,求めようとする変位波の利用の目的によっても異なる。すなわち,真の地震動のフィルタで取去られる部分を最小にし,かつ各振動数成分におけるS/Nを一定水準に維持しようとすれば,地震波形ごとにフィルタのパラメタを変えて,取去る振動数成分の範囲を変える必要がある。一方,多少誤差の含まれる割合が多くても,いくつかの地震波形に対して同一のフィルタを施すことが必要な場合もある。例えば,地震波ごとにフィルタのパラメタを変えると,水平・上下の各成分ごとに異なったフィルタを通して波形を見ることになるが,この場合に,上下,水平の各成分を比較するには,やや困難が伴なうと思われる。また,相異なる地点で得られた記録を比較しようとする場合にも,同様であろう。
このようなことから,「港湾地域強震観測年報」のように汎用性の高い資料を提供しようとしている場合には,どちらか一方の立場を選択するということは適当でないと思われる。地震波形によっては,取去る振動数の範囲の微小な相違が,得られる変位波に大きく影響するものも少なくないと思われるので,この両方の方法により変位波を求めることは,得られた変位波形の信頼性を検討する上でも,意味のあることと思われる。
(6) フィルタの妥当性の評価の方法の現状
フィルタによって得られた変位波が,どの程度真の変位波に近いかという点からの評価は,現在までのところ十分に行なわれていない。
例えば,振動台による妥当性の検討は,変位波の測定が容易であるという点ではすぐれているが,検討に使用する変位波が真の地震動変位の性質をどの程度近似しているかが必ずしも明らかではないため,フィルタの妥当性の検討としては十分ではない。例えば,フィルタにより取除かれる振動数成分を全く含まない変位波を振動台への入力として用いれば,結果はきわめて良いものであろう。しかし,フィルタにより取除かれるような長周期成分を変位波として優勢に含むような波形を,振動台への入力として用いれば,結果が思わしくないのは明らかである。
フィルタの妥当性の検討には,外からの情報,特に地震の真の変位波の性質についての情報や実測が必要とされる。ところが加速度波形から変位波形を求めようとする一つの目的は,精密な変位波形の実測データがない現状で,実測データの代用品を提供し,それを理論的考察の検討に用いるということである。このような現状において,絶対的な基準と対比するという形の十分な評価が行なわれ得ないのは,止むを得ないことである。
(7) 計算方法の細部について
(刀H 数字化記録端の処理
Caltechにおいては,先にふれたように,記録端の部分で発生するフィルタの応答をおさえるために,人工的にデータを追加して,フィルタリングを行なっている20)。このようなフィルタの応答は既に7.3区分的ゼロ線補正のところでふれたように,区分的にシフトしている記録では,記録端にかぎらず,その接続点で必ず発生する。ここで積分の対象としている加速度記録は,このような応答を最小限におさえるという配慮から,区分的ゼロ線補正を既に行なってあるので,記録端におけるフィルタの応答をおさえるために人工的なデータを追加する必要はない。
(刀ァ ゼロ線補正としての直線のあてはめ
Trifunacの方法19)あるいは,久保・佐藤の方法29)では,フィルタリングを行なう前に,あらかじめ時間tの一次関数を,加速度波形にあてはめて補正を行なっている。Trifunacの方法は,さらに,速度波形についても直線のあてはめを行ない加速度波形を補正するとともに,一部の計算プロセスをくりかえすというようなやや複雑な方法を採っている19,20)。
ここで,積分の対象としている加速度記録は,数字化のためコピーを作るものについても,密着コピーがされるので,固定線と波形との相対位置のゆがみは極めて小さいものと思われる。したがって,固定線補正により波形の全体としての回転は,ほぼ完全に補正されるので,1次関数の1次の項は補正する必要がない。仮に,1次関数で補正を行なうとすれば,記録に含まれる低振動数成分の影響により,逆に誤差を増大させる恐れがある。1次関数の定数項は,先にふれた区分的ゼロ線補正により補正される。
8.3 採用する方法
先に述べた各種方法の比較における考察に従って,一定のフィルタをすべての地震波に適用する方法と,フィルタにパラメタを導入し,地震波ごとにこのパラメタを考える方法との2つの方法により,加速度波形を補正し,これを積分して速度波形及び変位波形を求める。
(1) 固定フィルタ法
フィルタの形としては,先に述べた「倉田の方法」に近いもので,基本的には気象庁の一倍変位計をシュミレートすることにより,変位を求める方法である。フィルタH1(f)は,次式により与えられる。
.png) ・・・ (8-8)
・・・ (8-8)
ここに、f0=1/6(Hz)
h=0.552
f1=0.1(Hz)
倉田のフィルタG4(f)と比較するため,2回積分と合成した形で図-8.5に示した。G4(f)よりも0Hz付近の減衰をゆるやかにして,波形のゆがみの度合を小さくするとともに,補助的に使用するG1(f)型のフィルタによる位相のずれを除いた点が,G4(f)と異なる点である。 ただし,一倍変位計のシュミレーションを行なうことにより一倍変位計で得られた変位波形との直接比較を容易にするため,フィルタによる位相のずれはそのまま残すこととした。
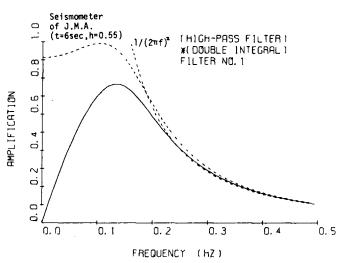
図-8.5 固定フィルタ法のフィルタと2回積分の合成
(2) パラメタ付きフィルタ法
フィルタの形は,先に示したH1(f)に比較的良く似たフィルタH2(f)とした。
.png) ・・・ (8-9)
・・・ (8-9)
2回積分と合成したものを図-8.6に示す。フィルタH1(f)と比べて,やや急激な減衰の仕方をする点と,位相の回転がない点が相違なる点である。
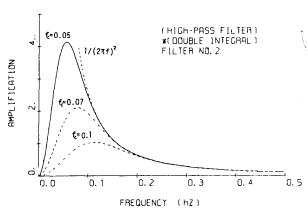
図-8.6 パラメタ付きフィルタ法のフィルタと2回積分の合成
フィルタのパラメタfcは,次式によって求まる値σが規定値Eに等しくなるように定めるものとした。ただし,数字化のために分割した区間の長さをT(秒)として,fc≧1/Tの条件を付加した。
.png) ・・・ (8-10)
・・・ (8-10)
ここに,X(f):計器特性補正前の加速度波形のフーリエ変換
f:振動数
T:数字化のために分割した区間の長さ(秒)
ただし,長さが区間ごとに異なる場合には,その最小値とする。
H2(f):先に述べたパラメタfcを含むフィルタ(式(8-9)参照)
S:数字化された記録の全長(秒)
この式は,やや見かけが複雑であるが,その意味する内容は単純である。その内容について説明する。まず,やや大まかな意味を説明するため,積分記号の中にある項のうち,中央にある[1-exp{-(fT)2}]4という項を除いておく。X(f)・[1-H2(f)]はフィルタH2(f)によって取除かれる低振動数成分を表わしている。したがって,│X(f)│2・[1-H2(f)]2は,この低振動数成分の絶対値の2乗である。このフィルタによって取除かれる低振動数成分の波形をy(t)(0≦t≦S)とすれば,(すなわち,X(f)・[1-H2(f)]のフーリエ逆変換をy(t)(0≦t≦S)とすれば),Parsevalの等式により
.png) ・・・ (8-11)
・・・ (8-11)
である。ここに,Sは数字化した記録の全長(秒)である。この式からわかるように,σ2は,式(8-10)の積分記号の中にある項のうちの中央にある[1-exp{-fT}2]4という項を除いて考えれば,フィルタによって取除く低振動数成分の2乗平均値に等しい。これが,σ2の大まかな意味である。(もっとも厳密に言えば,y(t)は(0≦t≦S)の外側でゼロとならないことが多いので,上の式は近似的な意味で成り立つと言える。)
先の補正項[1-exp{-fT}2]4は,次のような背景のもとに導入した。積分を行なう段階では数字化された記録は既に様々な補正を施されているが,なお残存する誤差として,区分的ゼロ線補正によっても補正されない区間ごとの微小なドリフトと,読取時のトレースにおける誤差が,低振動数成分に含まれる。このうちの区間ごとの微小なドリフトによる誤差は,トレースにおける誤差ほど安定した性質を持ってない恐れがあるので,この誤差は,フィルタによって除かれる低振動数成分の大きさを計算する場合には除いておく方が安全であると思われる。そこで,この部分をあらかじめ先のフィルタH2(f)の形で除いておくこととしたものである。このときのフィルタのパラメタfcは数字化のために分割した区間の長さ(の最小値)をT(秒)として,fc=1/Tとした。これがσ2の意味である。
つぎにフィルタのパラメタを,このような形で,フィルタによって取去る振動数成分の大きさが一定になるように決めたねらいについて説明する。
6.記録の数字化とその精度において行なった検討から,低振動数の誤差は,ホワイトノイズに近い性質を持ち,その大きさは,数字化の対象とされる波形によってやや変動するものの,その変動の程度は数字化の対照とされる波形の大きさの変動の程度よりは小さいという性質がわかった。しかし,これらの性質は,特に定量的な面においては,すべての記録について適用できるほどに確かであるとは言えない。それにもかかわらず,地震加速度波として,低振動数成分が優勢に含まれているならば,これらの誤差は無視し得るし,逆に,加速度波として低振動数成分がわずかしか含まれない場合には,低振動数の誤差が積分して求めた変位波において卓越するという性質は,はっきりと認められる。
そこでの性質をフィルタのパラメタfcの決定に反映させようというのが,σの大きさによってfcを定めるというねらいである。さて,その反映の仕方であるが,もし,誤差が大きさ一定のホワイトノイズっであるならば,振動数ごとに見たS/Nは,真の波形の振動数成分の大きさに比例する。したがって,スペクトルの大きさが一定のレベルを超える成分のうち最低の振動数を目安にフィルタのパラメタを決めることができる。しかし実際に含まれる誤差の大きさや性質は,このようなパラメタの決定法が適用できるほど都合のよい形はしていないことは既に述べた通りである。σの大きさによってfcを決定するという方法は,今ふれたS/Nの大きさをもとにしてfcを決めるという方法よりは,やや安定な動作を示す。言いかえれば,fcが与えられた波形に対して変化する変化の仕方はややにぶい。しかし,フィルタを固定する方法に比べれば,地震波ごとに追随する"やわらかさ"があると言える。このように,パラメタ付きフィルタ法による積分法も,実は誤差の大きさと真の波形の大きさの割合だけをもとにしてパラメタを決定するのでは・|・v佑・ぐ譴弔梁填┛討任△襪噺世┐襦・br>
さて,フィルタによって取去られる低振動数成分の大きさσを規定する値Eとしては,やや便宜的ではあるが,6.記録の数字化とその精度における検討例についての誤差の大きさをもとにして,次のような値とした。
SMAC-B2強震計の記録の場合:E=0.5(gal)
ERS強震計の記録の場合:E=0.05p(gal)
ただし,pは強震計の感度で,単位は(gal/mm)であるものとする。
(3) 計算方法の細部の補足
(刀H フーリエ変換
計器特性補正,フィルタリング,積分は,すべて周波数領域において行なう。このため,計器特性補正の前にフーリエ変換を行なう。この計算は,記録の数字化された部分の全長の外側に,適当な長さの区間を補なってFFTにより行なう。これは,リンク効果30)をさけるための処置であり,フィルタのインパルス応答の有意な長さの分だけ補う必要がある。
低振動数成分を取除くフィルタのインパルス応答は,一般的に,時刻0においてはデルタ関数状のパルスとなるので,このパルスを除いた応答の大きさについて,それが有意であるかどうかを判断した方がよいと思われる。そこで,フィルタのインパルス応答のかわりに,フィルタによって取去られる低周波成分のみをとり出すフィルタを考え,このフィルタのインパルス応答を検討の対象とした。この応答を,図-8.7と図-8.8に,それぞれ固定フィルタ法とパラメタ付きフィルタ法において用いられるフィルタについて示した。ただし,図-8.7において10Hzの成分が著しいのは,計算のために考慮した振動数の範囲を10Hzまでに制限したための計算誤差であるが,今行なおうとしている検討には大きな妨げとはならないと思われる。パラメタ付きフィルタ法において用いられるフィルタについては,式(8-9)を見ればわかるように,応答の長さは,フィルタのパラメタfcに反比例する。fcの最小値は既に説明したように,数字化のために分割した区間の長さをT(秒)とすれば,1/Tである。Tの大きさは,SMAC-B2強震計の記録の場合には,約30秒,ERS-B強震・|・ct記録の場合には,約35秒,ERS-C強震計の記録の場合には,約17.5秒である。図-8.8には,fc=1/30(Hz)の場合を示した。
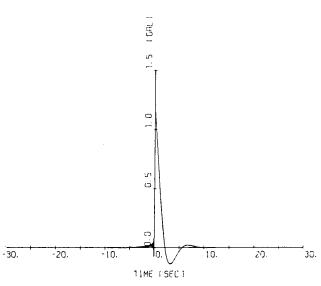
図-8.7 固定フィルタ法のフィルタのインパルス応答
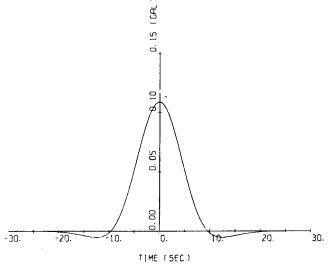
図-8.8 パラメタ付きフィルタ法のフィルタのインパルス応答(fc=1/30(Hz)
応答は,正負の両方向に発生するが,補われるゼロの区間においては,この応答が相互に重なり合っても対象とされる波形の区間には影響がない。
したがって,補うべきゼロの区間の長さは,時刻0から正または負のどちらか長い方の応答が有意である時刻までの長さとすればよい。有意であるかの判断は,応答の最大値の約1%の値以上である場合を有意として行なった。
結論として,SMAC-B2強震計の記録の場合には,20秒以上,ERS-B強震計の記録の場合には,24秒以上,ERS-C強震計の記録の場合には,12秒以上のゼロ区間を補うものとした。さらに,ゼロ区間の長さは,与えられた計算機の容量内で,計算時間が最小となるように定めるものとした。
(刀ァ 積 分
積分は,積分される波形に0Hzの成分が含まれていなければ,周波数領域においては1/2πfiなるフィルタに対応する。0Hzの成分が含まれていて,かつ区間を定めた積分の場合には,積分された0Hzの成分は,0Hz以外の振動数範囲にまで広がる。
ここで積分の対象とされる波形は,既に述べたフィルタにより補正されたもので,0Hzの成分を含まない波形であるから,1/2πfiなるフィルタにより積分できる。初期速度あるいは初期変位は,0Hz成分が積分された波形に含まれないという性質から自動的に定まる。ただし,ここでいう0HZの成分として考えるものは,加速度ゼロの区間を補った全体としての区間についての0Hzの成分である。
(4) 速度波形・変位波形の計算例
一般に,取去る低振動数の範囲を様々に変えたフィルタを,いくつかの地震記録の例に適用してその結果を見るという事例研究は,誤差を含んだ地震記録の低振動数成分が,どのような性質を持っているかという点については重要な情報を与えてくれる。したがって,パラメタ付きフィルタ法のパラメタを決定する値Eを定めるにあたっては,いくつかの事例研究を行ない。おおまかな見当をつけることに利用した。
しかし,このような事例研究は,真の地震波形の成分がどのような性質を持っているか,あるいは低振動数の誤差がどのような性質がありどの程度の大きさであるのか,という点については,地震波の性質に関して外部から何らかの情報が補われない限り,ほとんど情報は与えてくれない。したがって,ここでは単に1つの地震波形に適用した例を示すにとどめる。これを図-8.9に示す。なお,この波形は既に述べた様々な補正を行なうため,既に述べた数字化の方法に従って,今回新たに数字化を行なったものである。この波形は,SMAC-B2強震計の記録でS-252EWであり,数字化は,3区間に分割して行なった。各区間長は,それぞれ30.15秒,24.88秒,35.10秒である。このデータを,7.記録の補正に述べた1次補正のプロセス(図-7.1参照)に従って補正して求めた加速度波形が,図の一番上に示したものである。つぎに,1次補正されたデータ(全長90.13秒)のうち,加速度の大きい部分35秒間(はじめの25秒間とおわりの30.13秒を省略)を取出して,計器特性補正や積分を含む2次補正のプロセス(図-7.2参照)に従って求めたものが,図の上から2番目以下に示したものである。したがって,この図においては数字化のために分割した区間の接続点は,5.15秒および30.03秒になっている。
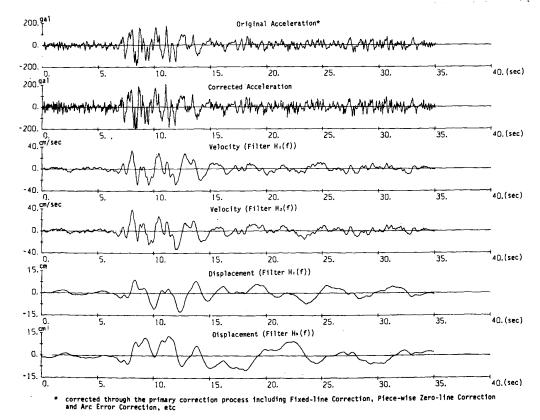
図-8.9 速度波形および変位波形の計算例(S-252EWの一部)
(5) 採用する方法の適用できる記録
ここに示した2つの方法は,既に述べた一連の補正のプロセスを経た補正値に適用するために提案した方法である。
港湾技術研究所で,1975年の年報として出版された記録を含めて,これ以前に公表された数字化記録は,このような一連の補正は行なっていない。
このような記録に対し,既に示した2つの方法を適用する場合には,次のような点に注意する必要がある。
(a) 固定保線を行なっていないこと
記録紙の蛇行,及び,数字化のために分割した区間ごとの記録紙の微小な回転による誤差が取除かれていない。固定フィルタ法の場合には,記録紙の蛇行が結果に与える影響は大きくないものと予想されるが,区間のつなぎ目付近で,区間ごとの回転の誤差により,フィルタの不自然な応答がでる可能性がある。パラメタ付きフィルタ法の場合,パラメタ決定のプロセスにおいて,このような誤差の大小により,誤差が大きいほどパラメタfcを小さくするという恐れがある。したがって,パラメタ付きフィルタ法は,一連の補正を行なっていない記録には適用すべきでない。
(b) 区分的ゼロ線補正を行なっていないこと
区間ごとに一定値を持つ段階状の誤差が残されている。したがって記録端を含めて区間のつなぎ目で,フィルタの不自然な応答が発生する可能性がある。図-8.10にその例を示した。一般にこの応答の大きさは,フィルタにより取去る成分の境界に相当する振動数の2乗に反比例する。また,Trifunacのフィルタのように,急激におとすフィルタであるほど,著しい影響がある。図-8.10では,気象庁の一倍地震計のシュミレーションに,式(8-1)のフィルタG1(f)(λ=0.2π)を補なって求めた変位波形を示した。図中の矢印は,区間のつなぎ目を示している。図-8.11には,参考のためステップ関数状の加速度から同じ方法で求めた変位波形を示した。
このように,(a),(b)2つの補正の行なわれていない記録から変位波形を求めるには,特にここで提案した2つの方法を用いる場合に限らず,十分な注意が必要である。
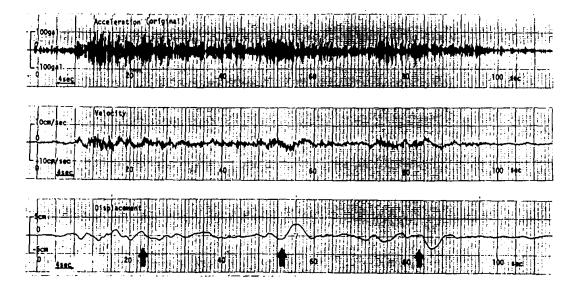
図-8.10 固定補正と区分的ゼロ線補正を行なわない加速度波形から求めた変位波(S-236NS)
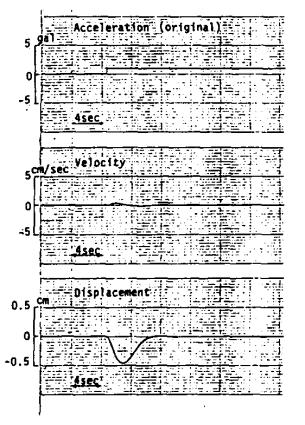
図-8.11 ステップ関数状の加速度波形から求めた速度・変位波形
前ページ
目次
次ページ
.png) ・・・ (8-1)
・・・ (8-1).png) ・・・ (8-1)
・・・ (8-1)
.png) ・・・ (8-2)
・・・ (8-2)
.png) ・・・ (8-3)
・・・ (8-3)
.png) ・・・ (8-4)
・・・ (8-4)
.png) ・・・ (8-5)
・・・ (8-5).png) ・・・ (8-6)
・・・ (8-6).png) ・・・ (8-7)
・・・ (8-7).png) ・・・ (8-8)
・・・ (8-8)
.png) ・・・ (8-9)
・・・ (8-9)
.png) ・・・ (8-10)
・・・ (8-10).png) ・・・ (8-11)
・・・ (8-11)



