S M A C | B 2 強 震 計 の 記 録 |
|||||
| SM.1 | 振子の特性 | S.2 | 仕 様 | 計器特性補正 | |
| SM.2 | 記録紙の送りの平均速度の仕様からのずれ | S.6 S.10X S.12X | タイムマーク | 時間間隔補正 | |
| SM.3 | 記録紙の送りむら | S.5 S.11X | タイムマーク | ||
| SM.4 | 記録紙の送りの立上り | S.4 | 検定結果 | 記録紙送りの立上り補正 | |
| SM.5 | 記録紙の蛇行と用紙セッティングの誤差 | S.7 S.11Y S.15 | 固定線 |
固定線補正 | |
| SM.6 |
円弧書きとペンの片寄り | S.8 S.9 |
仕様と円弧の記録 | 円弧補正 | |
| SM.7 | Y軸設定の誤差 | S.16 |
地震波の性質 | 区分的ゼロ線補正 | |
| SM.8 |
数字化装置とオペレータの読取り誤差 | S.13 S.14 S.17 | 検定結果と地震波の性質 | フィルタリング | |
E R S 強 震 計 の 記 録 |
ER.1 | 振子の特性 | E.2 | 仕 様 | 計器特性補正 |
| ER.2 | ガルバノメータの特性 | E.4 | 仕 様 | ||
| ER.3 |
ガルバノメータ・ボックスの振動 | E.6 | ボックスの振動波形 | ||
| ER.4 | 記録紙の送りの平均速度の仕様からのずれ | E.9 E.11X | タイムマーク | 時間間隔補正 | |
| ER.5 | 記録紙の送りむら | E.8 | タイムマーク | ||
| ER.6 | 記録紙の送りの立上り | E.7 | 検定結果 | ||
| ER.7 | 記録紙の蛇行と用紙セッティングの誤差 | E.10 E.14 | 固定線 | 固定線補正 | |
| ER.8 | Y軸設定の誤差 | E.15 | 地震波の性質 | 区分的ゼロ線補正 | |
| ER.9 | 数字化装置とオペレータの読取り誤差 | E.12 E.13 | 検定結果と地震波の性質 | フィルタリング | |
以上で、補正を行なわない誤差の種類についての説明をおわる。最後に、ERS強震計の記録の補正の項目で表-7.1に掲げなかった項目を追加する。項目の名称は、「平滑化」とする。ERS強震計の記録の数字化におけるサンプリングの間隔は、ERS-B強震計の記録の場合0.005秒、ERS-C強震計の場合0.0025秒である。これまでに得られた記録のうち、最も高い卓越振動数を示すものの例(M-106)では、20数Hz程度の卓越振動数であった。
この例から見て、サンプリングの間隔は最終的には50Hzまでをカバーできる0.01秒間隔とすれば十分であると思われる。数字化において、この間隔よりずっと密なサンプリング間隔を採ったのは、数字化における50Hz以上の誤差を地震波形から分離することをねらったためである。平滑化は、この50Hz以上の成分を取除くことを目的として行なう。
この平滑化により、データを0.01秒ごとにまびいても、50Hz以下の成分に50Hz以上の成分の誤差が重なるということがなくなる。平滑化は、内容としては、フィルタリングに含まれるが、後に説明するようにその方法と、補正の順序において占める位置が、フィルタリングとは異なっているので、ここでは独立した項目として追加した。
以上、補正の項目をあらためて列記すれば、次のとおりである。
○SMAC-B2強震計の記録の補正の項目
計器特性補正
時間間隔補正
記録紙送りの立上り補正
固定線補正
円弧補正
区分的ゼロ線補正
フィルタリング
○ERS強震計の記録の補正の項目
計器特性補正
時間間隔補正
固定線補正
区分的ゼロ線補正
フィルタリング
平滑化
(3) 補正の順序
7.2 固定線補正
なお,先に触れた数字化装置のアームの蛇行については,ピアノ線とテグスとを数字化装置上に直線になるように張力を加えて固定し,それぞれの直線をトレースすることにより,アームの蛇行はほとんどないことを確認した経験があることを付け加えておく。
ただし,区間端において,区間端からの距離がt0(sec)より小さい範囲では,区間端からの距離S(sec)に対応して,式(7-1)において,α=5/S2のようにαを決めなおして移動平均を行なうこととした。
補正の順序を考えるには、それぞれの補正の方法の性質のうち、順序を決定するために必要な性質を明確にする必要がある。そこで、ここでは、補正の順序を決定するために必要な性質について必要最小限触れながら、補正の順序を説明することとする。
(刀H SMAC-B2強震計の記録の補正の順序
計器特性補正は、正しい時間間隔で与えられたデータを扱うものとする。したがって、時間軸に関する補正、すなわち、時間間隔補正、記録紙送りの立上り補正、円弧補正は、計器特性補正の前に行なっておく必要がある。
フィルタリングとの順序関係は、周波数領域で考えれば明らかなように順序交換可能である。残る項目の固定線補正と区分的ゼロ線補正との順序関係については、一まず保留しておく。
時間間隔補正は、時間に比例したパラメタを持つデータから補間により、一定時間間隔(0.01秒間隔)のデータを求めるものとする。このパラメタとしては、記録紙上のX座標(時間軸座標)が考えられるが、SMAC-B2強震計の記録の場合、このX座標は、円弧書きのために時間に比例していない。したがって、時間間隔補正に先だって円弧補正を行なっておく必要がある。ただし、ここで行なう円弧補正は、記録ペンの片寄りも含めて、円弧書きを直線書きに補正するものとする。
記録紙送りの立上り補正は、直線書きに補正された波形をもとに、記録紙の送りの立上り部分について、補正を行なうものとする。このような方法であれば、記録紙送りの立上りの検定結果が利用できるからである。したがって、円弧補正は、立上り補正の前に行なっておく必要がある。
時間間隔補正と記録紙送りの立上り補正の順序関係は、両者が記録の異なった部分を対象としているので交換可能である。
区分的ゼロ線補正は、一本の波形の数字化のためのコピーが2枚以上にわたる場合には、2枚目以後の部分についても、円弧書きペンの片寄りの影響を、円弧補正によって除くことができるように、円弧補正の前に行なう必要がある。
最後に、固定線補正と区分的ゼロ線補正の順序関係を考える。区分的ゼロ線補正の方法が7.3 区分的ゼロ線補正で説明するように、波形に含まれる低振動数成分が、補正結果に悪影響を及ぼす方法であるので、固定線補正を先に行なって、低振動数の誤差を除いておく必要がある。
以上の考察から、SMAC-B2強震計の記録の場合の補正は、次の通りとする。
1. 固定線補正
2. 区分的ゼロ線補正
3. 円弧補正
4. 記録紙送りの立上り補正
5. 時間間隔補正
6. 計器特性補正
7. フィルタリング
(刀ァ ERS強震計の記録の補正の順序
時間間隔補正、計器特性補正、フィルタリングの順序関係については、既にSMAC-B2強震計の記録の補正の順序で検討したとおりである。また、固定線補正の区分的ゼロ線補正との順序関係についても既に述べた。
平滑化の位置について考える。平滑化に先立って、区分的ゼロ線補正を行なって、数字化のために分割した区間の接続点における不連続性を取除いておく必要がある。不連続点があると、平滑化のためのフィルタの適当でない応答が発生するため、不連続点付近の波形をゆがめる恐れがあるためである。一方、平滑化は時間間隔補正の前に行なうことにより、補間によって0.01秒間隔のデータにまびくことによって、50Hz以上の成分が、見かけ上50Hz以下の振動数成分の形をとって誤差として入り込むのを防ぐことができる。
以上の考察から、ERS強震計の記録の補正の順序は次のとおりとする。
1. 固定線補正
2. 区分的ゼロ線補正
3. 平滑化
4. 時間間隔補正
5. 計器特性補正
6. フィルタリング
図-7.1〜図-7.2にSMAC-B2強震計の記録と、ERS強震計の記録の補正の流れを示す。図-7.1には、計器特性補正の前の段階までの補正プロセスを1次補正と名付けて示した。図-7.2には,計器特性補正及びフィルタリングを中心としたプロセスを2次補正と名付けて示した。
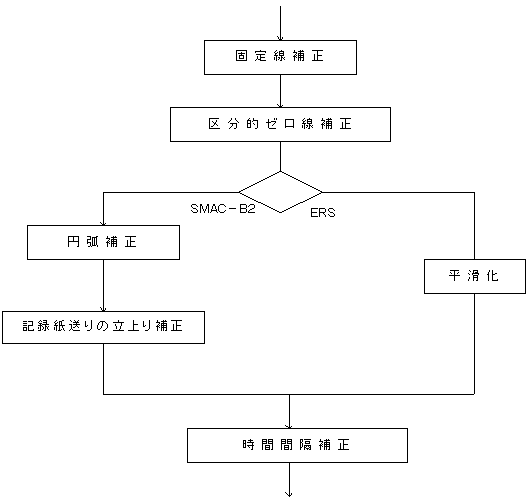
図-7.1 一次補正のプロセス
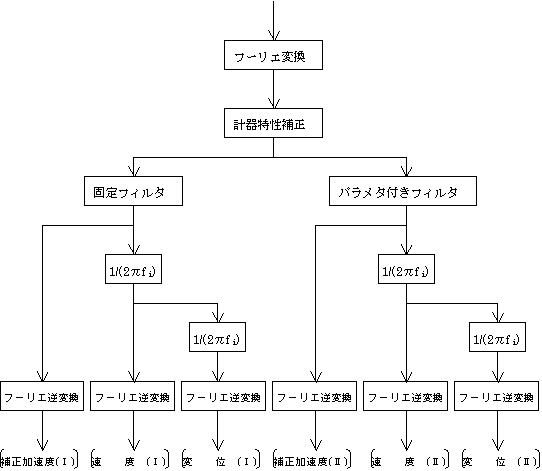
図-7.2 二次補正と積分のプロセス
(1) 補正の目的
記録紙の蛇行や,数字化装置のアーム蛇行,記録紙のセッティングにおいて発生する記録紙全体の微小な回転の誤差を取除くことを目的とする。
記録紙の蛇行などの誤差は大まかに言えば低振動数の誤差であるから,その大部分はフィルタリングにより取除くことができる。それにもかかわらず,固定線のデータを利用して補正するのは,次にあげるいくつかの理由による。
刀H 記録紙の蛇行は,数字化のために分割した区間の両端においては,見かけ上やや高い振動数成分を含む。これは,既に説明したように,記録紙のセッティングが,記録紙の蛇行に沿って行なわれるからである。視覚的な表現を使えば,もとのなめらかな蛇行の成分が,区間の接続点で折り曲げられるためこの析曲がった部分の蛇行の成分は,なめらかな成分のみを取除くフィルタリングでは取除けないのである。
刀ァ 記録紙のセッティングにおいて発生する区間ごとの微小な回転の誤差は,区間端部分において高振動数成分を優勢に含むので,低振動数成分のみを取除くフィルタリングによっては,完全に補正できない。
唐H 区分的ゼロ線補正においては,補正前のデータに含まれる低振動数成分が,数字化のために分割した区間ごとのドリフト(区間ごとに一定値をとる誤差)のみによって構成されているものと仮定して補正を行なう。したがって,あらかじめ区間ごとに蛇行のような低振動数の誤差を取除いておく必要がある。
唐ァ 低振動数成分を取除くフィルタリングのうち,後に説明するパラメタ付きフィルタによるフィルタリングでは,フィルタリングを行なう前のデータの低振動数成分に含まれる誤差が,記録紙の蛇行や区間ごと回転を含まない方が,パラメタの決定が適正に行なわれる。したがって,あらかじめ固定線により補正を行なっておくことが望ましい。
ここにあげた理由のうち,唐Hと唐ァは,これから説明する一連の補正方法が一体となって行なわれて,はじめてその効果を発揮することの一つの例として見ることもできる。
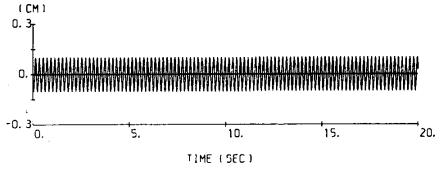
しかし,今あげた理由はもしも記録紙の蛇行などが十分に小さいことがわかっていれば,意味がなくなり,補正を行なう必要はないことになる。そこで図-7.3に固定線の数字化の結果の例を示す。簡単な試算によってもわかるように,この例のような大きさの蛇行を含む加速度波形を積分して変位波を求めようとすると,この蛇行の成分が非常に大きな影響を与える。したがって,一般に蛇行の大きさの程度はこの例から見て,補正を行なうに値する大きさであると考えられる。
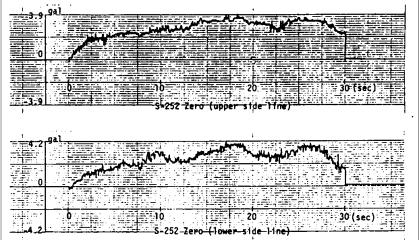
図-7.3 固定線の数字化の例(S-252)
(2) 補正の方法
補正の方法の概要は,次のとおりである。
1.記録の数字化において,同じセッティングの状態で地震波形と固定線とを数字化する。
2.固定線を平滑化する。
3.地震波形の数値から,平滑化された固定線の数値を引く。
以下に,SMAC-B2強震計の記録の場合と,ERS強震計の記録の場合に分けて,補正の詳細を説明する。
(刀H SMAC-B2強震計の記録の補正
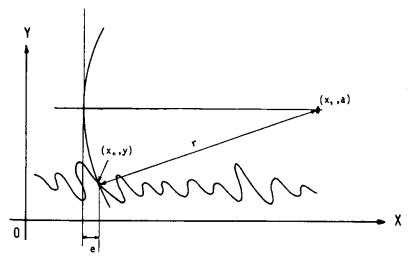
SMAC-B2強震計の記録には固定線が2本挿入されている。この固定線を描くペンの位置と,地震波形を描くペンの位置とは,記録紙の送りの方向に4〜8mm程度ずれている。(固定線のペンの位置の方が,記録紙の送られる方向にずれている。)
記録紙の蛇行は,記録紙の全体的な動き(記録紙送りと直角方向への動き)により発生すると思われるので,波形の数値から引くべき固定線の数値は,ペンの位置のずれを考慮して波形の数値に対応させる必要がある。一方,コピー作製時の振幅方向へのせん断変形のようなひずみや,数字化装置のアームの蛇行の誤差を除くためには,同一のX座標を持つデータを対応させる必要がある。ただし,アームの蛇行は先に述べたとおり,ほとんどないことが確認されている。
記録紙の蛇行の大きさとコピー作製時の振幅方向へのせん断変形の大きさの関係は必ずしも明らかではないが,ここでは,記録紙の蛇行を重視し,ペンの位置のずれを考慮して対応関係を定めるものとした。
固定線は,波形と同じく0.1mm間隔(0.01秒に相当)で数字化を行なう,しかし,6.記録の数字化とその精度において検討した例からもわかるように約0.2Hz以上の成分は数字化の誤差の占める割合が多いので,高い振動数成分は,平滑化により取除くこととした。固定線の平滑化は,時間領域で,次のような重み関数による移動平均により行なうこととした。
.png) ・・・ (7-1)
・・・ (7-1)
ここに、-1.png)
-2.png)
記録紙上には3本の地震波形にはさまれるように2本の固定線が描かれているが,記録紙上の両端にある2成分(水平成分)の波形を補正するための固定線は,それぞれの成分に最も近い固定線とした。また,中央に描かれる成分(上下成分)の波形を補正するための固定線は,2本の固定線の平均値とした。これは,記録紙の部分的なひずみの影響を可能なかぎり取除くことをねらったためである(図-6.1参照)。
(刀ァ ERS強震計の記録の補正
ERS強震計の記録には,固定線が振幅方向に2mm間隔で記録紙一面に描かれている。オシログラフの記録紙は,SMAC-B2強震計の記録紙よりも部分的な変形に対して強いので,ほぼ中央にある1本の固定線を数字化する。ERS強震計のオシログラフでは,固定線と波形を描く光線の記録紙上の像は,波形の像の方が約5mm記録紙送りの方向に進んでいる。そこで,SMAC-B2強震計の記録の補正と同じく,このずれを考慮して,波形と固定線の数字化を行い,両者を対応させる。
固定線の数字化間隔は,加速度波形の場合と同じく,0.1mm間隔とする。数字化の後,SMAC-B2強震計の記録の固定線の場合と同様にして,平滑化を行なう。最後に,この平滑化された固定線の数値を,加速度波形の数値から引くことにより補正を行なう。
7.3 区分的ゼロ線補正
(1) 補正の目的
数字化装置のY軸のゼロ点の設定の誤差を取除くことを目的とする。Y軸のゼロ点の設定の誤差は,数字化のために分割されてできた区間ごとに独立にはいる。したがって,全体としては,区分的に一定値をとる段階状の誤差となる。この誤差を補正するという意味で,区分的ゼロ線補正という名称をつけた。
このような階段状の誤差は低い振動数の成分だけを取り去るようなフィルタをかけても,階段のカドの部分が残されてしまう。特に,フィルタをかけた後に積分を行なう場合には,このカドの部分の影響が著しい。したがって,最終的にフィルタにより低振動数成分を除くとしても,あらかじめY軸のゼロ点の設定の誤差の値を推定して取除いておくことが必要である。
(2) 補正の方法
ここでは,真の加速度波形をほぼ無限に近い長さで考えた時のその平均値がゼロであるものと仮定して補正を行なう。この仮定は,例えば震源となった断層近くの点の加速度波形については当てはまらないが,このような場合を除けば,おおむね妥当であると思われる。
Y軸のゼロ点の設定の誤差は,全体としては階段状の誤差であり,低振動数成分の含まれる割合が大きい。そこで,固定線補正後のデータに含まれる低振動数成分を考える。低振動数成分としては,この場合数字化のために分割した区間の長さの程度か,それ以上の周期の成分を考えるものとする。すなわち,SMAC-B2強震計の記録又はERS-B強震計の記録の場合約30秒以上,ERS-C強震計の記録の場合,約15秒以上の周期の成分である。この程度の低振動数成分を構成するものは,Y軸のゼロ点の設定の誤差の他に,地震波形の一部と波形のトレースにおける誤差の一部が含まれる。ここでは,この程度の低振動数成分が,すべてY軸のゼロ点設定の誤差により成るものと仮定してY軸のゼロ点の設定の誤差の値を推定する。
低振動数成分のみを取出すような操作は,適当な重みつきの移動平均により行なうことができる。移動平均の平均幅をちょうど数字化のために分割した区間の長さにとれば,移動平均の後に得られた波形で,この区間の中央の点の値は他の区間のデータとは無関係に定まる。したがって,この移動平均により得られる低振動数成分が,すべてY軸のゼロ点の設定の誤差により成るものと仮定すれば,移動平均後の波形で各区間の中央の点の値とY軸の設定の誤差の値とは,一対一に対応する。さらに,この移動平均後の区間中央の点の値が,実はY軸の設定の誤差に値に一致することが言える。このことは,無限の長さの定数値関数と,ある区間で同じ定数値をとり,その他の領域ではゼロであるような関数とを考えてみるとわかりやすい。前者は0Hzの成分のみを持つ関数だから,重みつき移動平均をしても同じ定数値の関数となる。ところが,後者の重みつき平均で求めた区間中央の点の値は,前者の任意の点における重みつき平均値と同じ値である。したがって,先に述べたことが言えた。
以上の考察から,補正の方法としては,各区間について区間内の各データに適当な重みをつけた平均を行ない,この平均値を対応する区間の全データから引くことにより行なう。重み関数は,仮にこれを移動平均の重みとして使った時に,できるだけ低い振動数成分しか通さないものが望ましい。これは先の考察からわかるように地震加速度波形に含まれる低振動数成分やトレースの誤差の低振動数の成分が,Y軸のゼロ点の設定の誤差の値の推定を妨げるのを防ぐためである。ここでは,重み関数として次のような関数を使うこととした。
.png) ・・・ (7-2)
・・・ (7-2)
ここに、
α=20/T2
T:数字化のために分割した区間の長さ(sec)
重み関数w(t)で,第一の式の定義域をすべての実数とした関数のフーリエ変換は,
.png) ・・・ (7-3)
・・・ (7-3)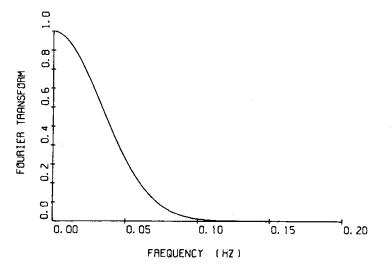
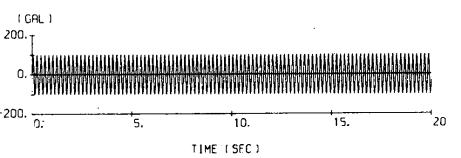
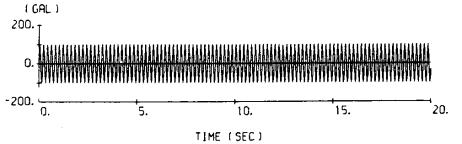
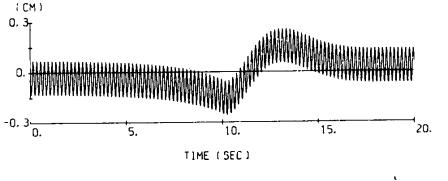
.png) ・・・(7-4)
・・・(7-4)