9. 補正された数値の評価
9.2 補正波形
9.1 フィルタリングの与える影響
これまでのところで,補正の方法について検討を行ない,現在最も妥当と考えられる補正方法を示し,個々の補正の精度についての評価を行なった。このようにして説明した補正のうち,フィルタリングは,普通の意味での補正とはやや異なる性格を持っているので,この点について,再度確認しておく。
フィルタリングは,低振動数あるいは高振動数の誤差を取除くという意味では,補正と呼んでも妥当である。しかし,地震動がフィルタにより影響される振動数範囲に成分を有しているときは,誤差とともに地震動そのものの成分を取除いてしまうという点で,逆に,別の形の誤差を導入しているのである。したがって,フィルタリングを行なう前の波形に含まれる誤差と,フィルタリングを行なって新たに導入された誤差の大きさの大小関係によっては,フィルタリングが誤差を増大させる場合もあり得る。例えば,関東大地震(大正12年9月1日)に伴なう地殻変動の観測値では,相模湾岸から房総半島にかけて,水平方向には2〜5m程度,上下方向には1〜2m程度の大きさの静的な変位が見られた31)。しかし,仮にこの地震動を相模湾岸で観測したとして,この記録に対してフィルタリングを行なえば,このような静的な変位は,ほとんどゼロとなってしまう。フィルタリングによって補正された補正波形が無条件に真の波形として取扱えないのは,この例によってもわかる。
フィルタリングにより達成できる目的は,実は真の波形を求めるというところからは一歩後退したもので,与えられた加速度波形から最大限の情報をとり出すというものである。具体的には,加速度波形に含まれる振動数成分のうち,信頼できる成分の範囲を定め,この部分のみを取出すということを目的としている。したがって否定的に言えば,真の波形(例えば真の変位波形)を求めることは,外から何らかの情報が補われない限り,断念していると言える。フィルタリングが普通の意味での補正とはやや異なる性格を持つと言ったのは,このような事柄を指している。もちろん,フィルタによって取去られる振動数の範囲に,地震動の成分がほとんど含まれていない場合には,フィルタリングは低振動数の誤差を取去るだけであるから,フィルタリングがあらゆる地震波形に対して悪影響を及ぼすというわけではない。しかし,フィルタリングの影響には,十分注意する必要があると思われる。
補正値はこのように,フィルタリングによって取出された"信頼できる成分"のみから成る。しかし,6.記録の数字化とその精度において検討したように,数字化における誤差は全ての振動数範囲に広がり,この"信頼できる成分"にも含まれている。
ただ,その含まれる割合が小さいだけである。したがって補正された数値を利用する場合には,フィルタリングの影響と同時にフィルタリングによって取出された部分に含まれる誤差の大きさについても,例えば,変位波形を利用する場合には考慮する必要がある。
(1) 補正加速度
(刀H SMAC-B2強震計の記録の場合
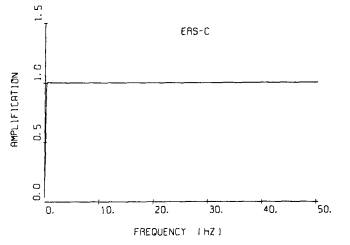
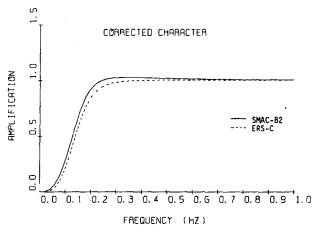
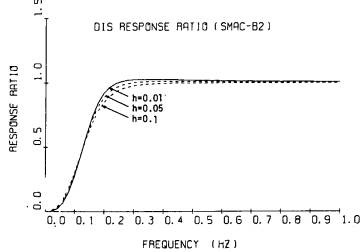
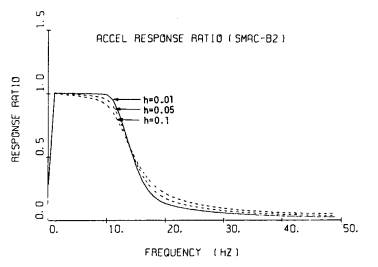
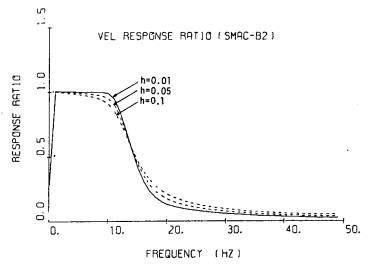
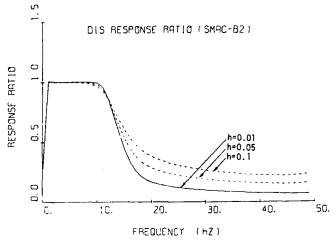
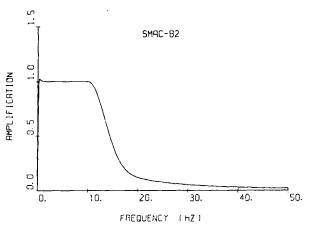
SMAC-B2強震計の記録の場合には,既に述べたように,計器特性を補正して求めた波形の10Hz以上の成分をフィルタリングにより小さくしている。ただし,フィルタによる補正は必要最小限にとどめた方が波形を人工的にゆがめる度合が小さいので,10Hz以上50Hzまでの成分もゼロとしてはいない。図-9.1に,フィルタリングにおいて使われるフィルタを示す。ただし,低い振動数成分を取去るフィルタの部分は,この図には,固定フィルタ法において用いられるフィルタを示した。(式(8-8)参照)この図を見ればわかるように,10Hz以上の成分が地振動に優勢に含まれていなければ,補正加速度はほぼ真の値と見てよい。しかし,地震動に10Hz以上の成分が優勢に含まれている場合には,フィルタの影響により,真の値よりも小さいことが予想される。